Chapter 5 Association of Words
In n-gram analysis, we look at the association of words using the consecutive words. Another way is to investigate how often any two words appear in a given comment. For example, if a comment mentioned that a professor was great, we might be interested in knowing what other words were mentioned in the same context. Therefore, for doing so, we would need to find all possible combinations of the words in the comments.
5.1 Pairwise association
To get all the pairs of words, we start by dividing the comments into individual words. We also removed stopwords to prepare for further analysis.
prof.tm <- unnest_tokens(prof1000, word, comments)
stopwords <- read_csv("data/stopwords.evaluation.csv")
prof.tm <- prof.tm %>% anti_join(stopwords)The function pairwise_count in the R package widyr can be used to count how many times a pair of words appear together in a comment. It checks each comment to see if a specific pair of words is in it. Note that for two words, the different orders are considered as two pairs in the output.
library(widyr)
# count words co-occurring within sections
word.pairs <- prof.tm %>% pairwise_count(word, id, sort = TRUE)
word.pairs
## # A tibble: 1,528,270 x 3
## item1 item2 n
## <chr> <chr> <dbl>
## 1 test easy 2600
## 2 easy test 2600
## 3 test hard 2064
## 4 hard test 2064
## 5 test study 2004
## 6 study test 2004
## 7 test lecture 1947
## 8 lecture test 1947
## 9 easy great 1591
## 10 great easy 1591
## # ... with 1,528,260 more rowsFor example, in total, we have 38157 pieces of comments. After removing the stopwords, there are a total of 8155 unique words in all of the comments. In total, there are 1,528,270/2 = 764,135 pairs of words. The pair of words “easy” and “test” appeared in 2,600 of all the comments.
For the word “test”, it co-occurs with more than 4,000 words. The top words included “easy”, “hard”, “study” and so on. This tells that when “test” is mentioned, a student would very much care about whether it’s “easy” or “hard”.
word.pairs %>% filter(item1 == "test")
## # A tibble: 4,337 x 3
## item1 item2 n
## <chr> <chr> <dbl>
## 1 test easy 2600
## 2 test hard 2064
## 3 test study 2004
## 4 test lecture 1947
## 5 test good 1459
## 6 test question 1414
## 7 test great 1401
## 8 test grade 1269
## 9 test note 1266
## 10 test book 1253
## # ... with 4,327 more rows5.2 Pairwise correlation
Pairs like “test” and “easy” are the most common co-occurring words in this data set. However, this might be because both “test” and “easy” are frequently used words. Therefore, we need a statistic in addition to the frequency count to quantify the tendency for a pair of words to be together in a comment. One such measure can be the phi coefficient to quantify the pairwise correlation. The idea is to examine how often they appear together relatively to how often they appear separately among all the comments.
The phi coefficient is a measure of the correlation between two binary variables. It is similar to the Pearson correlation coefficient in its interpretation as a Pearson correlation coefficient estimated for two binary variables will return the phi coefficient. The square of the phi coefficient is a scaled chi-squared statistic by its sample size for a 2 \(\times\) 2 contingency table, that is \(\phi = \sqrt{\chi^2/n}\). If the absolute value of a phi coefficient is between 0 to 0.3, it denotes very little or no correlation; between 0.3 to 0.7, weak correlation; and between 0.7 to 1.0, a strong correlation.
The phi coefficient for a pair of word “x” and “y” is calculated based on the following 2 \(\times\) 2 contingency table. In the table,
- \(n_{11}\) is the total number of comments with both word x and word y in it.
- \(n_{10}\) is the total number of comments with word x but without word y.
- \(n_{01}\) is the total number of comments with without word x but with word y.
- \(n_{00}\) is the total number of comments with neither word x nor word y.
- \(n_{1.}\) is the total number of comments with word x.
- \(n_{0.}\) is the total number of comments without word x.
- \(n_{.1}\) is the total number of comments with word y.
- \(n_{.0}\) is the total number of comments without word y.
- \(n_{..}\) is the total number of comments.
| With word y | without word y | Total | |
|---|---|---|---|
| With word x | \(n_{11}\) | \(n_{10}\) | \(n_{1.}\) |
| Without word x | \(n_{01}\) | \(n_{00}\) | \(n_{0.}\) |
| Total | \(n_{.1}\) | \(n_{.0}\) | \(n_{..}\) |
With the information, the phi coefficient can be calculated as
\[ \phi = \frac{n_{11}n_{00}-n_{10}n_{01}}{\sqrt{(n_{1.}n_{0.}n_{.0}n_{.1})}}. \]
The phi coefficient for each pair of words is calculated below using the function pairwise_cor of the wider package. Note that we only did the calculation for words that appear at least 1,000 times in the comments. Furthermore, the phi coefficient would change according to the selection of the words.
word.phi <- prof.tm %>% group_by(word) %>% filter(n() >= 1000) %>% pairwise_cor(word,
id, sort = TRUE)
word.phi %>% print(n = 20)
## # A tibble: 8,556 x 3
## item1 item2 correlation
## <chr> <chr> <dbl>
## 1 attention pay 0.873
## 2 pay attention 0.873
## 3 extra credit 0.776
## 4 credit extra 0.776
## 5 hour office 0.662
## 6 office hour 0.662
## 7 highly recommend 0.507
## 8 recommend highly 0.507
## 9 guide study 0.480
## 10 study guide 0.480
## 11 answer question 0.391
## 12 question answer 0.391
## 13 midterm final 0.387
## 14 final midterm 0.387
## 15 help willing 0.306
## 16 willing help 0.306
## 17 book read 0.288
## 18 read book 0.288
## 19 test study 0.212
## 20 study test 0.212
## # ... with 8,536 more rowsFrom the output, we can see that most of the phi coefficients are small. Only two coefficients are larger than 0.7 and 5 coefficients are between 0.3 and 0.7.
5.3 Visualization
By putting the phi coefficient together, we can get a correlation matrix of the words. The correlations can be visualized through a network plot to help understand how the words are related. In the code below, the arrow used in the network plot is defined through a. We only plot the pair of words with correlation greater than 0.1.
a <- arrow(angle = 30, length = unit(0.1, "inches"), ends = "last", type = "open")
word.phi %>% filter(correlation > 0.1) %>% graph_from_data_frame() %>% ggraph(layout = "fr") +
geom_edge_link(aes(color = correlation, width = correlation), arrow = a) + geom_node_point() +
geom_node_text(aes(label = name), vjust = 1, hjust = 1)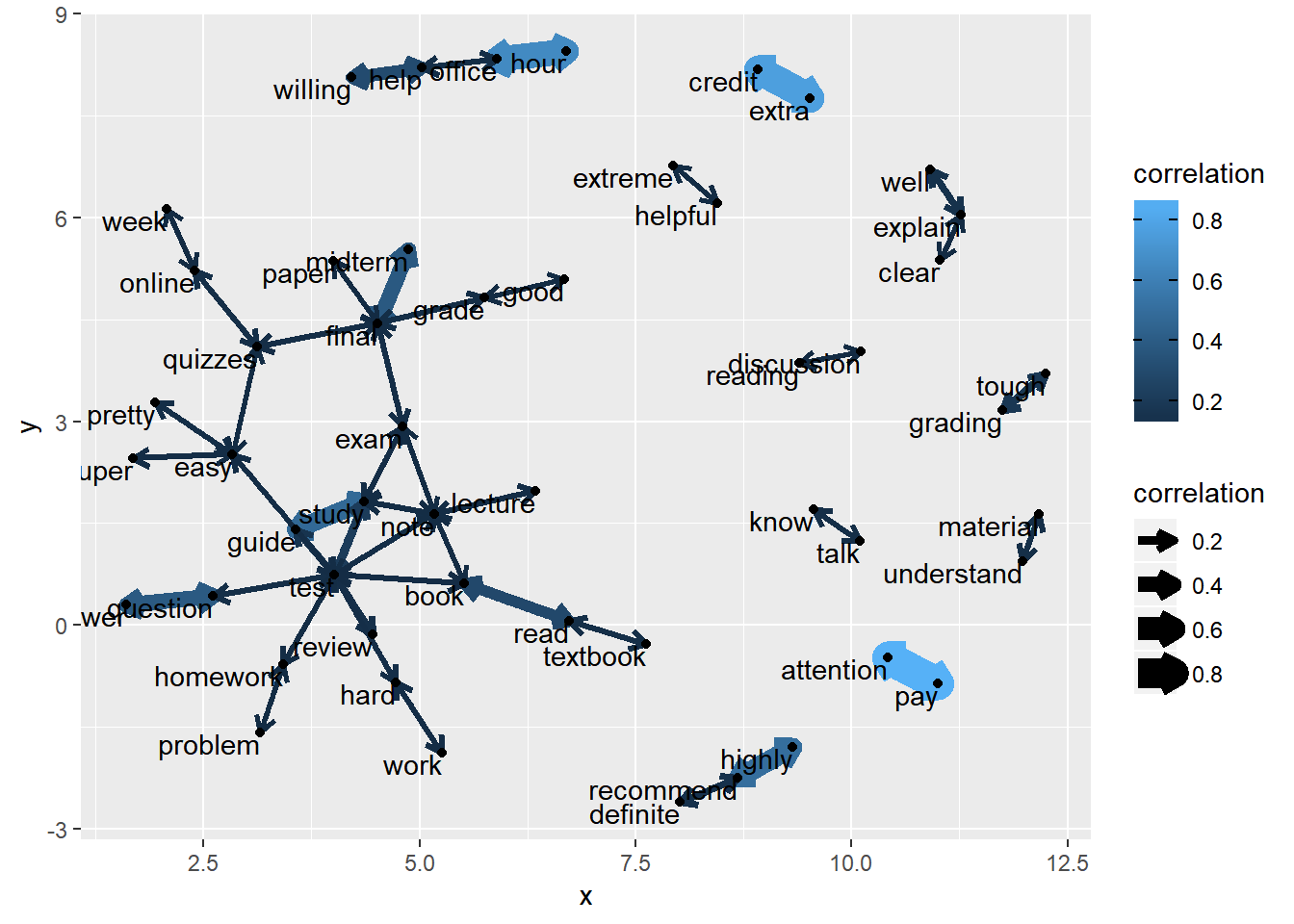
5.4 Association Rules
Pairwise count and pairwise correlation tell how a pair of words are related. One might be also interested in how more than one words are related to another word. For example, if a student mentioned words such as “easy” and “great”, he/she would be more like to recommend a professor and therefore mention the word “recommend”. This can be investigated using a method called “Market basket analysis” in which the association rules can be identified.
Market basket analysis is often used in understanding shopping behaviors. For example, through analyzing shopping transactions, we can understand which items are frequently bought together. For example, if one buys eggs, it’s highly likely she/her would buy milk. In our text mining, we can understand which words come together. Market basket analysis is conducted by mining association rules. To do so, the R package arules can be used.
The package arules has its own data format - the transaction data format. The data should have at least two columns - the transactionID and the items in that transaction. An example is given below. The data set has three transactions. In each transaction, customers bought different items.
For our data, the items would be individual words. We can convert the tidytext data to the transaction data format easily. The following code first converts the data into a document-term matrix (cast_dtm), then to a regular matrix (as.matrix), and then to the transaction data format [(]as(prof.mat, "transactions")]. Note that we also removed very sparse terms before converting data. After that, there are a total of 113 words left and the sparsity of the matrix is 94%.
prof.dtm <- prof.tm %>% count(id, word) %>% cast_dtm(id, word, n)
prof.subset <- removeSparseTerms(prof.dtm, 0.98)
prof.subset
## <<DocumentTermMatrix (documents: 38149, terms: 113)>>
## Non-/sparse entries: 258925/4051912
## Sparsity : 94%
## Maximal term length: 13
## Weighting : term frequency (tf)
prof.mat <- as.matrix(prof.subset)
prof.arules <- as(prof.mat, "transactions")
prof.arules
## transactions in sparse format with
## 38149 transactions (rows) and
## 113 items (columns)
inspect(prof.arules[1:10])
## items transactionID
## [1] {assignment,
## best,
## dont,
## like} 1
## [2] {best,
## clear,
## expect,
## explain,
## help,
## homework,
## mathematics,
## question,
## willing} 2
## [3] {clear,
## explain,
## homework,
## better,
## don't,
## great,
## topic,
## understand,
## work} 3
## [4] {help,
## willing,
## difficult,
## extreme,
## grade,
## hour,
## know,
## material,
## note,
## office,
## prepare,
## tough} 4
## [5] {don't,
## topic,
## understand,
## know,
## answer,
## talk,
## well,
## worst} 5
## [6] {mathematics,
## work,
## definite,
## hard,
## learn,
## love,
## semester,
## time} 6
## [7] {great,
## tough,
## learn,
## time,
## easy,
## favorite,
## life} 7
## [8] {help,
## homework,
## work,
## knowledgeable,
## problem,
## study,
## week} 8
## [9] {mathematics,
## well,
## worst,
## lecture} 9
## [10] {like,
## clear,
## great,
## hour,
## office,
## time,
## helpful} 10In the data, each transaction is one comment. For example, in the first transaction/comment, there are three words - assignment, best, and like. For the second transaction/comment, there are nine words or items.
We can also check the basic information of the matrix. From the output of summary, we can see
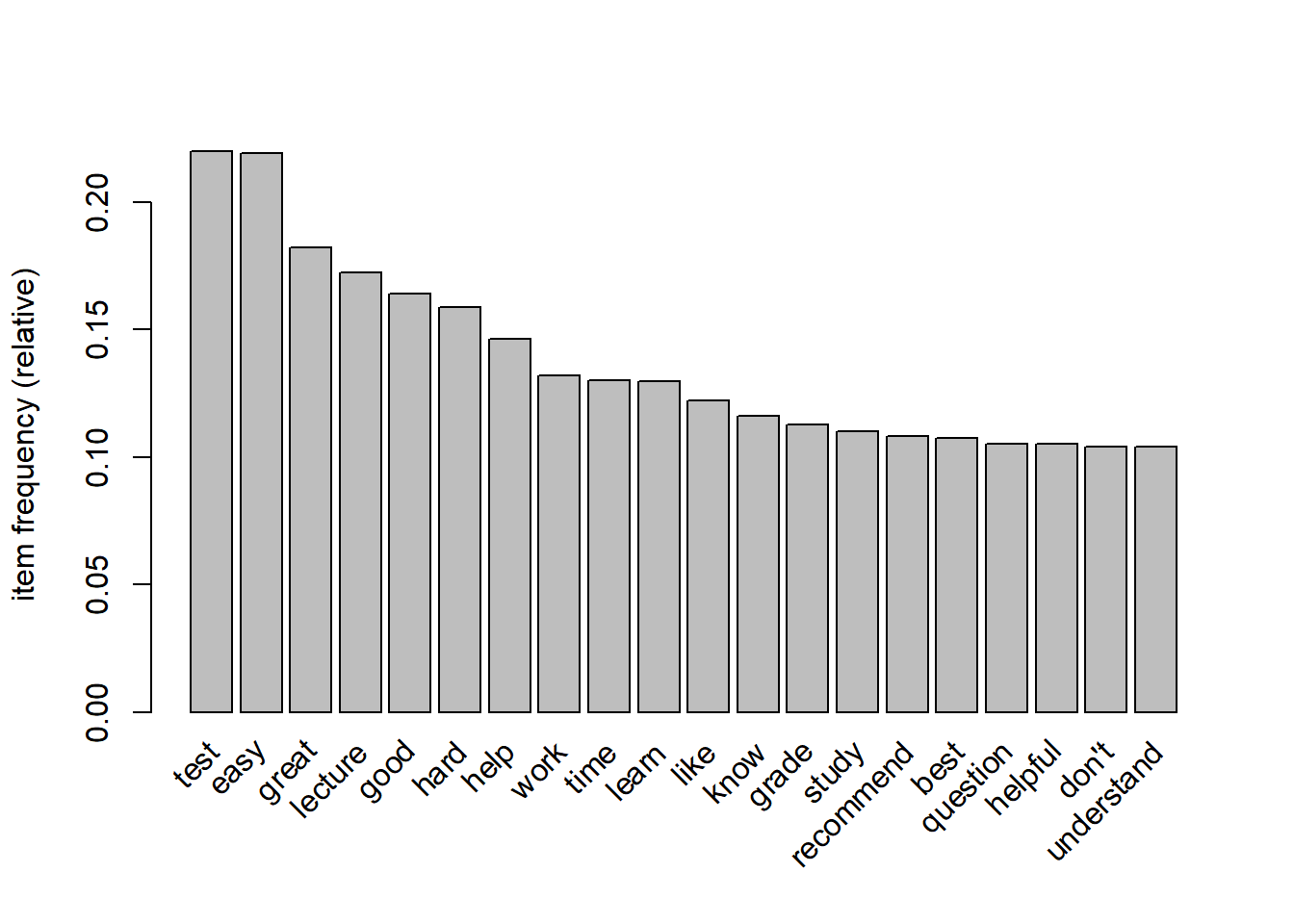
- There are 38,149 transactions (the total number of comments) and 113 items (words).
- The most frequent items (words) are test, easy, great, lecture, and good.
- The majority of comments/transactions have around 6 words/items based on the element length distribution.
summary(prof.arules)
## transactions as itemMatrix in sparse format with
## 38149 rows (elements/itemsets/transactions) and
## 113 columns (items) and a density of 0.06006374
##
## most frequent items:
## test easy great lecture good (Other)
## 8388 8356 6946 6567 6255 222413
##
## element (itemset/transaction) length distribution:
## sizes
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
## 271 1083 2119 3096 3697 4129 4359 4134 3923 3296 2736 2031 1413 842 529 283
## 16 17 18 19 20 21 23
## 114 53 24 12 3 1 1
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 4.000 7.000 6.787 9.000 23.000
##
## includes extended item information - examples:
## labels
## 1 assignment
## 2 best
## 3 dont
##
## includes extended transaction information - examples:
## transactionID
## 1 1
## 2 2
## 3 35.4.1 Visualization
We can plot the top words/items in the data using the function itemFrequencyPlot.
We can also plot the items for each transaction. In the plot below, a square is plotted if a transaction/comment has the item/word in the x-axis.
5.4.2 Mining rules
The R package arules has the Apriori algorithm to identify association rules in the data. A rule is to tell which word (or an item such as food) is frequently associated (bought) with another word (item). We could use the notation that Word A -> Word B to mean from Word A, we can expect Word B. THe Apriori algorithm tries to find this kind of rules.
The basic usage of the apriori function is given below.
apriori(data, parameter = list(support=0.1, confidence=0.8)
In using it, we need to decide on support and confidence. Support measures the frequency of the words, calculated as the proportion of occurrence of certain words over the total number of observations. Suppose there are two words A and B, then the support of A and B is
\[ Support (A \& B) = \frac{Number\ of\ comments\ with\ both\ A\ and\ B}{Total\ number\ of\ comments} = P\left(A \cap B\right) \]
Confidence is like a conditional probability defined as
\[ Confidence (A -> B) = \frac{Number\ of\ comments\ with\ both\ A\ and\ B}{Total\ number\ of\ times\ with\ A} = \frac{P\left(A \cap B\right)}{P\left(A\right)} \] It means given A, what is the probablity to have B in the same comment/transaction.
We can also define something called lift based on support and confidence. The higher the lift, the higher the chance of A and B occurring together.
\[ lift = \frac{Confidence (A->B)}{Support(A) \times Support(B)} = \frac{P\left(A \cap B\right)}{P\left(A\right)P\left(B\right)} \]
Oftentimes, we need to try different support and confidence to identify a set of meaningful rules. For example, when we set support to 0.005 and confidence to 0.6, we get 84 rules, with 10 rules having two words, 70 rules with 3 words and 4 rules with 4 words.
prof.rules <- apriori(prof.arules, parameter = list(support = 0.005, confidence = 0.6,
minlen = 2))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.6 0.1 1 none FALSE TRUE 5 0.005 2
## maxlen target ext
## 10 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 190
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[113 item(s), 38149 transaction(s)] done [0.01s].
## sorting and recoding items ... [113 item(s)] done [0.00s].
## creating transaction tree ... done [0.01s].
## checking subsets of size 1 2 3 4 done [0.02s].
## writing ... [84 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
prof.rules
## set of 84 rulessummary(prof.rules)
## set of 84 rules
##
## rule length distribution (lhs + rhs):sizes
## 2 3 4
## 10 70 4
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.000 3.000 3.000 2.929 3.000 4.000
##
## summary of quality measures:
## support confidence lift count
## Min. :0.005007 Min. :0.6065 Min. : 2.758 Min. : 191.0
## 1st Qu.:0.005806 1st Qu.:0.7859 1st Qu.: 8.592 1st Qu.: 221.5
## Median :0.006907 Median :0.8546 Median :16.930 Median : 263.5
## Mean :0.010057 Mean :0.8385 Mean :16.266 Mean : 383.7
## 3rd Qu.:0.009384 3rd Qu.:0.9112 3rd Qu.:22.041 3rd Qu.: 358.0
## Max. :0.038035 Max. :0.9784 Max. :28.373 Max. :1451.0
##
## mining info:
## data ntransactions support confidence
## prof.arules 38149 0.005 0.6All 84 rules are presented below. For the first rule, the support is about 0.025, the confidence is about 0.92 and the lift is 8.36. So it means if there is the word “guide” in the comment, then it would have the word “study” in 92% of the time in the comment. For Rule 11, if there are words “exam” and “guide”, it would have “study” in the comment 95% of the time.
inspect(prof.rules)
## lhs rhs support confidence lift count
## [1] {guide} => {study} 0.025112061 0.9202690 8.356901 958
## [2] {midterm} => {final} 0.019450051 0.6469050 9.681749 742
## [3] {office} => {hour} 0.024797505 0.8197574 19.352057 946
## [4] {pay} => {attention} 0.029489633 0.8978452 26.327360 1125
## [5] {attention} => {pay} 0.029489633 0.8647194 26.327360 1125
## [6] {highly} => {recommend} 0.034417678 0.8950239 8.289455 1313
## [7] {willing} => {help} 0.028257621 0.6857506 4.692502 1078
## [8] {answer} => {question} 0.031770164 0.6579805 6.254995 1212
## [9] {credit} => {extra} 0.038035073 0.7950685 16.289510 1451
## [10] {extra} => {credit} 0.038035073 0.7792696 16.289510 1451
## [11] {exam,guide} => {study} 0.005347453 0.9488372 8.616327 204
## [12] {great,guide} => {study} 0.005006684 0.9502488 8.629145 191
## [13] {lecture,guide} => {study} 0.006815382 0.9352518 8.492959 260
## [14] {easy,guide} => {study} 0.008597866 0.9452450 8.583706 328
## [15] {study,guide} => {test} 0.015229757 0.6064718 2.758261 581
## [16] {test,guide} => {study} 0.015229757 0.9667221 8.778739 581
## [17] {easy,guide} => {test} 0.006055205 0.6657061 3.027661 231
## [18] {easy,midterm} => {final} 0.006946447 0.6992084 10.464536 265
## [19] {office,helpful} => {hour} 0.006867808 0.8851351 20.895433 262
## [20] {hour,helpful} => {office} 0.006867808 0.8424437 27.849554 262
## [21] {help,office} => {hour} 0.009384256 0.8063063 19.034517 358
## [22] {help,hour} => {office} 0.009384256 0.8384075 27.716124 358
## [23] {great,office} => {hour} 0.005190175 0.9000000 21.246349 198
## [24] {great,hour} => {office} 0.005190175 0.7388060 24.423491 198
## [25] {office,lecture} => {hour} 0.006238696 0.8913858 21.042992 238
## [26] {office,test} => {hour} 0.005845501 0.8168498 19.283418 223
## [27] {note,pay} => {attention} 0.005478518 0.9675926 28.372552 209
## [28] {note,attention} => {pay} 0.005478518 0.9207048 28.031899 209
## [29] {study,pay} => {attention} 0.005766862 0.9523810 27.926503 220
## [30] {study,attention} => {pay} 0.005766862 0.8835341 26.900195 220
## [31] {good,pay} => {attention} 0.006946447 0.9397163 27.555140 265
## [32] {good,attention} => {pay} 0.006946447 0.9201389 28.014668 265
## [33] {hard,pay} => {attention} 0.005530944 0.8755187 25.672684 211
## [34] {hard,attention} => {pay} 0.005530944 0.8940678 27.220904 211
## [35] {great,pay} => {attention} 0.005845501 0.9291667 27.245795 223
## [36] {great,attention} => {pay} 0.005845501 0.8544061 26.013360 223
## [37] {lecture,pay} => {attention} 0.007994967 0.9413580 27.603280 305
## [38] {lecture,attention} => {pay} 0.007994967 0.8495822 25.866489 305
## [39] {easy,pay} => {attention} 0.008859996 0.9521127 27.918637 338
## [40] {easy,attention} => {pay} 0.008859996 0.8989362 27.369127 338
## [41] {test,pay} => {attention} 0.009672600 0.9584416 28.104218 369
## [42] {test,attention} => {pay} 0.009672600 0.9088670 27.671482 369
## [43] {best,highly} => {recommend} 0.006081418 0.9280000 8.594871 232
## [44] {helpful,highly} => {recommend} 0.005819288 0.9367089 8.675530 222
## [45] {learn,highly} => {recommend} 0.005583370 0.9181034 8.503212 213
## [46] {help,highly} => {recommend} 0.005688222 0.9041667 8.374133 217
## [47] {great,highly} => {recommend} 0.009095913 0.9353100 8.662573 347
## [48] {lecture,highly} => {recommend} 0.005373666 0.8613445 7.977527 205
## [49] {easy,highly} => {recommend} 0.008964848 0.9243243 8.560828 342
## [50] {test,highly} => {recommend} 0.005557157 0.8617886 7.981640 212
## [51] {willing,great} => {help} 0.007785263 0.6734694 4.608463 297
## [52] {willing,easy} => {help} 0.005635796 0.6803797 4.655750 215
## [53] {willing,test} => {help} 0.006395974 0.7283582 4.984061 244
## [54] {help,answer} => {question} 0.005190175 0.6804124 6.468241 198
## [55] {great,answer} => {question} 0.005399879 0.7152778 6.799684 206
## [56] {answer,lecture} => {question} 0.007182364 0.7248677 6.890849 274
## [57] {answer,easy} => {question} 0.006631891 0.6356784 6.042984 253
## [58] {final,credit} => {extra} 0.005059110 0.8976744 18.391719 193
## [59] {final,extra} => {credit} 0.005059110 0.8772727 18.338125 193
## [60] {exam,credit} => {extra} 0.007129938 0.8369231 17.147035 272
## [61] {exam,extra} => {credit} 0.007129938 0.8242424 17.229602 272
## [62] {grade,credit} => {extra} 0.007549346 0.8275862 16.955739 288
## [63] {grade,extra} => {credit} 0.007549346 0.8445748 17.654621 288
## [64] {study,credit} => {extra} 0.007549346 0.8753799 17.934946 288
## [65] {study,extra} => {credit} 0.007549346 0.8470588 17.706546 288
## [66] {work,credit} => {extra} 0.005137749 0.7313433 14.983896 196
## [67] {work,extra} => {credit} 0.005137749 0.6666667 13.935708 196
## [68] {help,credit} => {extra} 0.006422187 0.8477509 17.368876 245
## [69] {good,credit} => {extra} 0.006736743 0.8056426 16.506155 257
## [70] {good,extra} => {credit} 0.006736743 0.7859327 16.428793 257
## [71] {hard,credit} => {extra} 0.006448400 0.7859425 16.102535 246
## [72] {hard,extra} => {credit} 0.006448400 0.7500000 15.677671 246
## [73] {great,credit} => {extra} 0.007785263 0.8510029 17.435504 297
## [74] {great,extra} => {credit} 0.007785263 0.7857143 16.424227 297
## [75] {lecture,credit} => {extra} 0.009567748 0.8548009 17.513320 365
## [76] {lecture,extra} => {credit} 0.009567748 0.8057395 16.842826 365
## [77] {easy,credit} => {extra} 0.013211355 0.8195122 16.790317 504
## [78] {easy,extra} => {credit} 0.013211355 0.8600683 17.978490 504
## [79] {test,credit} => {extra} 0.015334609 0.8251058 16.904920 585
## [80] {test,extra} => {credit} 0.015334609 0.8565154 17.904222 585
## [81] {easy,study,guide} => {test} 0.005924140 0.6890244 3.133714 226
## [82] {easy,test,guide} => {study} 0.005924140 0.9783550 8.884376 226
## [83] {easy,test,credit} => {extra} 0.005924140 0.8401487 17.213122 226
## [84] {easy,test,extra} => {credit} 0.005924140 0.9076305 18.972711 226The rules can be roughly divided into three categories: actionable, trivial, and inexplicable. Actionable means we identify something that is truly useful. Trivial means the rule does not add much to the existing knowledge. Inexplicable means it is hard to explain a rule and further investigation is needed. How to use these rules needs the input of subject experts.
## lhs rhs support confidence lift count
## [1] {note,pay} => {attention} 0.005478518 0.9675926 28.37255 209
## [2] {test,pay} => {attention} 0.009672600 0.9584416 28.10422 369
## [3] {note,attention} => {pay} 0.005478518 0.9207048 28.03190 209
## [4] {good,attention} => {pay} 0.006946447 0.9201389 28.01467 265
## [5] {study,pay} => {attention} 0.005766862 0.9523810 27.92650 220
## [6] {easy,pay} => {attention} 0.008859996 0.9521127 27.91864 338
## [7] {hour,helpful} => {office} 0.006867808 0.8424437 27.84955 262
## [8] {help,hour} => {office} 0.009384256 0.8384075 27.71612 358
## [9] {test,attention} => {pay} 0.009672600 0.9088670 27.67148 369
## [10] {lecture,pay} => {attention} 0.007994967 0.9413580 27.60328 305